게시 됨 업데이트 됨Algorithm

탐욕법(Greedy Algorithm)

탐욕법(Greedy Algorithm)이란?

미래를 고려하지 않고 각 단계에서 최적의 해를 찾아 모든 단계를 진행할 경우 최선의 결과에 도달한다고 생각하는 알고리즘.

특징

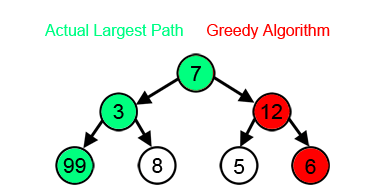
  • 전체적인 최적해를 보장할 수 없다.
  • 선택한 것을 번복하지 않는다.
  • 직관적

예시, 최소 신장 트리

예시, 거스름돈 최소 개수 반환

거슬러줄 돈(w)에서 동전(10, 50, 100, 500)을 뺐을 때 그 값이 가장 작은 경우의 동전을 우선 반환한다.

여기서 “뺀 값이 가장 작은 경우가 최적의 해”라는 게 이 문제에서 가장 근본적인 명제이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 거스름돈 최소 개수 반환
int change = w; //입력: 거슬러줄 돈
int n500, n100, n50, n10 = 0;
while(change >= 500) {
    change -= 500; n500++;
}
while(change >= 100) {
    change -= 100; n100++;
}
while(change >= 50) {
    change -= 50; n50++;
}
while(change >= 10) {
    change -= 10; n10++;
}
return n500 + n100 + n50 + n10;

단, 200원에 대해 동전이 위의 네 가지 밖에 없다면 최종해는 100*2로 “2”겠지만, 160원짜리 동전이 만들어진다면  160*1 + 10*4로 “5”가 나오기 때문에 탐욕법으로 최적해를 찾을 수 없게 된다. 이처럼 모든 상황에서 최적해를 찾을 수 있는 유연한 방법이 아니다.

동적 계획법과 비교된다.

동적 계획법(Dynamic Programming)이란, 전체를 바라보고 그것을 여러 개의 하위 문제들로 나누어 각 하위 문제들의 답을 이용해 최종 답을 내는 것이다.(복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법)

동적 계획법 특징

  • 큰 문제 안에 작은 문제가 중첩되어 있는 문제를 해결하는 데 사용. 예를 들어, 피보나치 수열.
  • 중첩되는 데이터라면 저장하고, 지속적으로 데이터를 참조한다.

피보나치 수열을 간단하게 코드화하면 아래와 같다.

1
2
3
4
5
public void fib(int n) {
  if (n == 0) return 0;
  else if (n == 1) return 1;
  else return fib(n-1) + fib(n-2);
}

이때, fib(5)를 구하려고 하면 fib(2)의 계산은 여러번 중복된다. 이로 인한 계산 속도의 저하를 막기 위해 fib(2)와 같이 중복되는 값은 배열에 저장하여 필요할 때 배열에 접근해서 값을 가져오는 방식이다.

중복계산이 줄어들기 때문에 시간 복잡도는 O(n)가 된다.

카테고리

광고

×